CTF | 2020 CISCN初赛 Z3&LFSR WriteUp

CTF WriteUp Z3
CTF
发布日期:   2020-08-27
文章字数:   3.1k
阅读时长:   15 分

引言

喵呜，好久没来写博客了咕咕咕（这就来除草了！

前不久水了一波 CISCN 线上初赛，感谢队友带我玩带我飞~

这里来写一写 Z3、LFSR 这两题的 WriteUp，顺便记录一下用到的 Z3、SageMath 求解工具喵。

Z3

首先丢进 IDA 看一看，首先将输入的 flag 分别存放在 v46 到 v87 变量内，而后是这些变量组成的线性方程，最后与 Dst 的结果比较，正确则输出 win。

其中Dst及其之后对应的那部分空间就是方程的值，将数据抠出来求解就完事了！

z3_1

z3_2

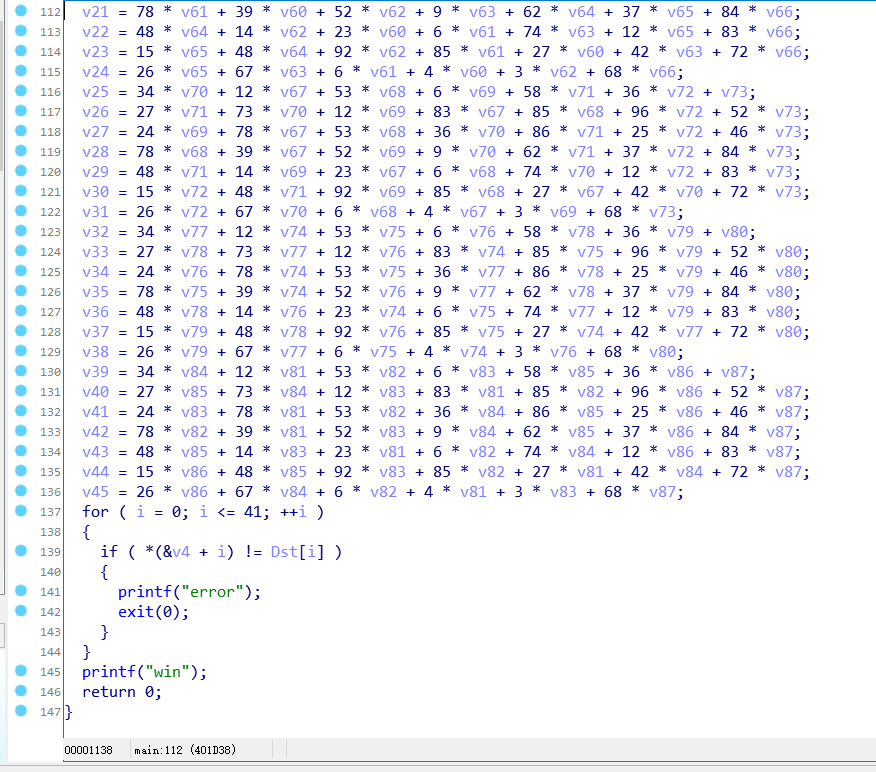
本来想用 MATLAB 之类来求解的，但看到题目名字叫 z3，搜了一下，果然有个叫 z3 的求解器，于是直接用它来约束求解即可。

而且这个 z3 还挺强大的亚子。。

from z3 import *

solver = Solver()
v46 = Int('flag[0]')
v47 = Int('flag[1]')
v48 = Int('flag[2]')
v49 = Int('flag[3]')
v50 = Int('flag[4]')
v51 = Int('flag[5]')
v52 = Int('flag[6]')
v53 = Int('flag[7]')
v54 = Int('flag[8]')
v55 = Int('flag[9]')
v56 = Int('flag[10]')
v57 = Int('flag[11]')
v58 = Int('flag[12]')
v59 = Int('flag[13]')
v60 = Int('flag[14]')
v61 = Int('flag[15]')
v62 = Int('flag[16]')
v63 = Int('flag[17]')
v64 = Int('flag[18]')
v65 = Int('flag[20]')
v66 = Int('flag[21]')
v67 = Int('flag[22]')
v68 = Int('flag[23]')
v69 = Int('flag[24]')
v70 = Int('flag[25]')
v71 = Int('flag[26]')
v72 = Int('flag[27]')
v73 = Int('flag[28]')
v74 = Int('flag[29]')
v75 = Int('flag[30]')
v76 = Int('flag[31]')
v77 = Int('flag[32]')
v78 = Int('flag[33]')
v79 = Int('flag[34]')
v80 = Int('flag[35]')
v81 = Int('flag[36]')
v82 = Int('flag[37]')
v83 = Int('flag[38]')
v84 = Int('flag[39]')
v85 = Int('flag[40]')
v86 = Int('flag[41]')
v87 = Int('flag[42]')
solver.add(v46 > 0)
solver.add(v46 < 128)
solver.add(v47 > 0)
solver.add(v47 < 128)
solver.add(v48 > 0)
solver.add(v48 < 128)
solver.add(v77 > 0)
solver.add(v77 < 128)
solver.add(v78 > 0)
solver.add(v78 < 128)
solver.add(v79 > 0)
solver.add(v79 < 128)
solver.add(v76 > 0)
solver.add(v76 < 128)
solver.add(34 * v49 + 12 * v46 + 53 * v47 + 6 * v48 + 58 * v50 + 36 * v51 + v52 == 0x4f17)
solver.add(27 * v50 + 73 * v49 + 12 * v48 + 83 * v46 + 85 * v47 + 96 * v51 + 52 * v52 == 0x9cf6)
solver.add(24 * v48 + 78 * v46 + 53 * v47 + 36 * v49 + 86 * v50 + 25 * v51 + 46 * v52 == 0x8ddb)
solver.add(78 * v47 + 39 * v46 + 52 * v48 + 9 * v49 + 62 * v50 + 37 * v51 + 84 * v52 == 0x8ea6)
solver.add(48 * v50 + 14 * v48 + 23 * v46 + 6 * v47 + 74 * v49 + 12 * v51 + 83 * v52 == 0x6929)
solver.add(15 * v51 + 48 * v50 + 92 * v48 + 85 * v47 + 27 * v46 + 42 * v49 + 72 * v52 == 0x9911)
solver.add(26 * v51 + 67 * v49 + 6 * v47 + 4 * v46 + 3 * v48 + 68 * v52 == 0x40a2)
solver.add(34 * v56 + 12 * v53 + 53 * v54 + 6 * v55 + 58 * v57 + 36 * v58 + v59 == 0x2f3e)
solver.add(27 * v57 + 73 * v56 + 12 * v55 + 83 * v53 + 85 * v54 + 96 * v58 + 52 * v59 == 0x62b6)
solver.add(24 * v55 + 78 * v53 + 53 * v54 + 36 * v56 + 86 * v57 + 25 * v58 + 46 * v59 == 0x4b82)
solver.add(78 * v54 + 39 * v53 + 52 * v55 + 9 * v56 + 62 * v57 + 37 * v58 + 84 * v59 == 0x486c)
solver.add(48 * v57 + 14 * v55 + 23 * v53 + 6 * v54 + 74 * v56 + 12 * v58 + 83 * v59 == 0x4002)
solver.add(15 * v58 + 48 * v57 + 92 * v55 + 85 * v54 + 27 * v53 + 42 * v56 + 72 * v59 == 0x52d7)
solver.add(26 * v58 + 67 * v56 + 6 * v54 + 4 * v53 + 3 * v55 + 68 * v59 == 0x2def)
solver.add(34 * v63 + 12 * v60 + 53 * v61 + 6 * v62 + 58 * v64 + 36 * v65 + v66 == 0x28dc)
solver.add(27 * v64 + 73 * v63 + 12 * v62 + 83 * v60 + 85 * v61 + 96 * v65 + 52 * v66 == 0x640d)
solver.add(24 * v62 + 78 * v60 + 53 * v61 + 36 * v63 + 86 * v64 + 25 * v65 + 46 * v66 == 0x528f)
solver.add(78 * v61 + 39 * v60 + 52 * v62 + 9 * v63 + 62 * v64 + 37 * v65 + 84 * v66 == 0x613b)
solver.add(48 * v64 + 14 * v62 + 23 * v60 + 6 * v61 + 74 * v63 + 12 * v65 + 83 * v66 == 0x4781)
solver.add(15 * v65 + 48 * v64 + 92 * v62 + 85 * v61 + 27 * v60 + 42 * v63 + 72 * v66 == 0x6b17)
solver.add(26 * v65 + 67 * v63 + 6 * v61 + 4 * v60 + 3 * v62 + 68 * v66 == 0x3237)
solver.add(34 * v70 + 12 * v67 + 53 * v68 + 6 * v69 + 58 * v71 + 36 * v72 + v73 == 0x2a93)
solver.add(27 * v71 + 73 * v70 + 12 * v69 + 83 * v67 + 85 * v68 + 96 * v72 + 52 * v73 == 0x615f)
solver.add(24 * v69 + 78 * v67 + 53 * v68 + 36 * v70 + 86 * v71 + 25 * v72 + 46 * v73 == 0x50be)
solver.add(78 * v68 + 39 * v67 + 52 * v69 + 9 * v70 + 62 * v71 + 37 * v72 + 84 * v73 == 0x598e)
solver.add(48 * v71 + 14 * v69 + 23 * v67 + 6 * v68 + 74 * v70 + 12 * v72 + 83 * v73 == 0x4656)
solver.add(15 * v72 + 48 * v71 + 92 * v69 + 85 * v68 + 27 * v67 + 42 * v70 + 72 * v73 == 0x5b31)
solver.add(26 * v72 + 67 * v70 + 6 * v68 + 4 * v67 + 3 * v69 + 68 * v73 == 0x313a)
solver.add(34 * v77 + 12 * v74 + 53 * v75 + 6 * v76 + 58 * v78 + 36 * v79 + v80 == 0x3010)
solver.add(27 * v78 + 73 * v77 + 12 * v76 + 83 * v74 + 85 * v75 + 96 * v79 + 52 * v80 == 0x67fe)
solver.add(24 * v76 + 78 * v74 + 53 * v75 + 36 * v77 + 86 * v78 + 25 * v79 + 46 * v80 == 0x4d5f)
solver.add(78 * v75 + 39 * v74 + 52 * v76 + 9 * v77 + 62 * v78 + 37 * v79 + 84 * v80 == 0x58db)
solver.add(48 * v78 + 14 * v76 + 23 * v74 + 6 * v75 + 74 * v77 + 12 * v79 + 83 * v80 == 0x3799)
solver.add(15 * v79 + 48 * v78 + 92 * v76 + 85 * v75 + 27 * v74 + 42 * v77 + 72 * v80 == 0x60a0)
solver.add(26 * v79 + 67 * v77 + 6 * v75 + 4 * v74 + 3 * v76 + 68 * v80 == 0x2750)
solver.add(34 * v84 + 12 * v81 + 53 * v82 + 6 * v83 + 58 * v85 + 36 * v86 + v87 == 0x3759)
solver.add(27 * v85 + 73 * v84 + 12 * v83 + 83 * v81 + 85 * v82 + 96 * v86 + 52 * v87 == 0x8953)
solver.add(24 * v83 + 78 * v81 + 53 * v82 + 36 * v84 + 86 * v85 + 25 * v86 + 46 * v87 == 0x7122)
solver.add(78 * v82 + 39 * v81 + 52 * v83 + 9 * v84 + 62 * v85 + 37 * v86 + 84 * v87 == 0x81f9)
solver.add(48 * v85 + 14 * v83 + 23 * v81 + 6 * v82 + 74 * v84 + 12 * v86 + 83 * v87 == 0x5524)
solver.add(15 * v86 + 48 * v85 + 92 * v83 + 85 * v82 + 27 * v81 + 42 * v84 + 72 * v87 == 0x8971)
solver.add(26 * v86 + 67 * v84 + 6 * v82 + 4 * v81 + 3 * v83 + 68 * v87 == 0x3a1d)

if(solver.check()):
    print(solver.model())

得到结果为：

[flag[8] = 55,
 flag[3] = 103,
 flag[1] = 108,
 flag[16] = 98,
 flag[15] = 51,
 flag[26] = 57,
 flag[11] = 52,
 flag[18] = 45,
 flag[9] = 49,
 flag[24] = 45,
 flag[22] = 49,
 flag[30] = 54,
 flag[14] = 54,
 flag[0] = 102,
 flag[25] = 57,
 flag[40] = 52,
 flag[10] = 100,
 flag[20] = 52,
 flag[23] = 56,
 flag[37] = 102,
 flag[39] = 54,
 flag[41] = 56,
 flag[7] = 49,
 flag[17] = 57,
 flag[4] = 123,
 flag[29] = 45,
 flag[2] = 97,
 flag[33] = 52,
 flag[5] = 55,
 flag[36] = 97,
 flag[12] = 51,
 flag[38] = 101,
 flag[27] = 48,
 flag[32] = 49,
 flag[31] = 101,
 flag[34] = 99,
 flag[42] = 125,
 flag[35] = 50,
 flag[28] = 101,
 flag[21] = 101,
 flag[13] = 45,
 flag[6] = 101]

即

[102, 108, 97, 103, 123, 55, 101, 49, 55, 49, 100, 52, 51, 45, 54, 51, 98, 57, 45, 1, 52, 101, 49, 56, 45, 57, 57, 48, 101, 45, 54, 101, 49, 52, 99, 50, 97, 102, 101, 54, 52, 56, 125]

而后利用 chr 把数字转换为字符即可得到 flag。

flag{7e171d43-63b9-4e18-990e-6e14c2afe648}

Z3 Introduction

简介

Z3 is a theorem prover from Microsoft Research. It is licensed under the MIT license.

If you are not familiar with Z3, you can start here.

Pre-built binaries for stable and nightly releases are available from here.

Z3 can be built using Visual Studio, a Makefile or using CMake. It provides bindings for several programming languages.

See the release notes for notes on various stable releases of Z3.

Z3 在工业应用中实际上常见于软件验证、程序分析等。然而由于功能实在强大，也被用于很多其他领域。CTF 领域来说，能够用约束求解器搞定的问题常见于密码题、二进制逆向、符号执行、Fuzzing 模糊测试等。此外，著名的二进制分析框架 angr 也内置了一个修改版的 Z3。

GitHub repo: https://github.com/Z3Prover/z3

Z3 - Slides: https://github.com/Z3Prover/z3/wiki/Slides

Z3 - guide ( English ): https://rise4fun.com/z3/tutorialcontent/guide

Z3 API/函数接口: http://z3prover.github.io/api/html/index.html

（Python 的 Z3 接口文档，guide-examples）

据说它可以解决所有的方程，当然如果有解的话。感觉就贼强大。

微软爸爸还是强啊（

安装

这里就以 python3 为例了。

pip3 install z3-solver

注意这里不是 pip install z3！！！（是我了嘤嘤嘤，我也不知道 pip 里的 z3 是什么玩意

使用

三步走：

  1. 定义未知量
  2. 添加约束条件
  3. 求解

注意：如果方程有多组解，z3 只会给出其中的一组解，因此可以尝试为方程添加约束条件，进一步限制解的范围，从而获得预期的一组解

Example:

首先看最简单的例子。

from z3 import *
x = Int('x')
y = Int('y')
solve(x > 2, y < 10, x + 2*y == 7)

运行得到

[y = 0, x = 7]

再来看稍微复杂一点的。

变量类型常用的包括 Int型（整数），Real型（有理数），BitVec型（位向量）。

解常用的方程一般是用 Int型，在求解位运算（如&, ^, |, >>, << 这些）用 BitVec型就很方便，包括下面的 LFSR 也可以用到。

求解方程组的话，需要先初始化一个Solver（约束求解器），

然后利用 add 方法依次往里面加入方程。

其次判断解是否存在
if solver.check() == sat:

最后求解
print(solver.model())

from z3 import *
x, y, z = Ints('x y z')  # 可以同时定义多个变量
s = Solver()
s.add('EQU1')
s.add('EQU2')
s.add('EQU3')

if solver.check() == sat:
    print(solver.model())

这道题里就用了这一方法来求解。

大概先写这么多，其他的还得慢慢学，可以参考下最后的拓展阅读喵~

LFSR

题目所给代码如下。

import random

from secret import flag

N = 100
MASK = 2**(N+1) - 1

def lfsr(state, mask):
    feedback = state & mask
    feed_bit = bin(feedback)[2:].count("1") & 1
    output_bit = state & 1
    state = (state >> 1) | (feed_bit << (N-1))
    return state, output_bit

def main():
    assert flag.startswith("flag{")
    assert flag.endswith("}")

    mask = int(flag[5:-1])
    assert mask.bit_length() == N
    
    state  = random.randint(0, MASK)
    print(state)
    
    outputs = ''
    for _ in range(N**2):
        state, output_bit = lfsr(state, mask)
        outputs += str(output_bit)
    
    with open("output.txt", "w") as f:
        f.write(outputs)

main()

这题让我想起了这学期卫星导航课做的实验，让我们利用不同抽头的移位寄存器生成伪随机序列，还有m序列什么的。

m序列是最长线性移位寄存器序列的简称，是一种伪随机序列、伪噪声(PN)码或伪随机码。可以预先确定并且可以重复实现的序列称为确定序列；既不能预先确定又不能重复实现的序列称随机序列；不能预先确定但可以重复产生的序列称伪随机序列。

它是由带线性反馈的移存器产生的周期最长的序列。一般来说，一个n级线性反馈移存器可能产生的最长周期等于(2^n -1)。

在通信领域有着广泛的应用，如扩频通信、卫星通信的码分多址（CDMA），数字数据中的加密、加扰、同步、误码率测量等领域。

Via Baidu baike

线性反馈移位寄存器（linear feedback shift register, LFSR）是指，给定前一状态的输出，将该输出的线性函数再用作输入的移位寄存器。异或运算是最常见的单比特线性函数：对寄存器的某些位进行异或操作后作为输入，再对寄存器中的各比特进行整体移位。

当时由于N较小，直接就用列表来写了，就是有点丑，后来想想可以用移位来实现。看了题目里面的 def lfsr(state, mask) 这一函数，发现写的就很妙啊。

当然还有这样的（2018 强网杯 streamgame1，2018 国赛 oldstreamgame）

def lfsr(R,mask):
    output = (R << 1) & 0xffffff
    i=(R&mask)&0xffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit
    return (output,lastbit)

话说回来，对于这题而言，分析可知，flag 括号内的字符是二进制位数为100位的整数。考虑到这题把 flag 作为 mask 而不是初始的状态 state，且初始 state 是随机给定的整数，LFSR 得到的伪随机序列最大重复周期为 $2^{100}-1$，爆破求解无法解出。

分析 LFSR 的逻辑可知，lfsr 函数内的输出位 $output bit = m_0x_0 + m_1x_1 + … + m_{99}x_{99}$（模二和），由于这是一个线性的方程，于是可以通过求解100个方程得到对应的系数m，也就得到了 flag。

Exp

output = "0100110011101111011111011010100111001010010100001111110110111101011110011111010010010111011100110111011001100001010010011101101000110110000011111011110000010100001001000011001011011011011001111110101111001010011011100010011110101100100101111001011100011110111101001010000000100100000111100101100100100000100110001111110011100110101000110100011001110110000110111111010111000001101110011001101111010110101000101011110111001011001111111000100100100011100100010101001100111011101111100110101011101101001001110010111011010011111001100001111111100001000001101101000001010100110011001101000101001010001001011000010111111100101111000000101000010110100110101001001100100011000111101000110011110101101111100110101010101000000001110010101001001111101001010111011110110001100101001111110111000110101011011010110101100011110010000011000110010111101010010000011101110111100011011110110001111010101011101100101101001111100100011000100101111011110001111100000110111000111111000111100000110011011011111110011111100010010110000010011100001010101011011101100011001100101100011001010010001101010011000000011110110111000000110001010010111110101011100000010100100001101011010101100110000101100010001010010111011000100001000001001110101011000010111000000010101100001010000010110110000111100011011000010111001111101110111010110000011001011101100000100000100010100100000010011010000111110010001111010000100011110000101111000110100010110101110001011101101100111000001110100100000000010011001110101110000001101100000001010111010011111000101101011001010011001101000111000010111111010101000011011001001110000011100100100010110101100001110110111001000001011111100101100011010010010110000011110100110000111011011010101110101001100110100101100101000100011001011000001011110010000011000110111011110011010001101100010010111110101101101110100111010000001101000011011010011110111101000000100011000000101001000000011010101010000100001110110000110011000111101011100100101111101111111110101000011010001101100010010100111000000010000101100100110101000001001011100011111001101001101100010100000111010101111011101111111101100000010000111110011101010100101110100101010100011110100100000111010001000100011010011100010011000001110110100110110010100100110111011001010010010100000110101110000011110010110100010101000110000111101011011010111101100111100101001101001101100111101000100101101100010111010010111100100111101101110101110011010110011111011111010000011000100010010101110001001000111111100100010100000001001010111010100010111001011011101110010110111110110100011111101110111011000111001010010110001001011011100110101111100100000101110000001011110011101110101101001011111100011001100111001011011001011011101000101100100011101000011101011010110010111111010011110111111111100001101101001101101111000100110010010100000100000100110100100110010000100101100000101010101000111110101001111111011011111101101110010100110000010110111001101110011101100001111111001110110010010011101111100111111000010011010010011100000001010011111111110001111110110110110001001001111011001101110110101100011010001111110010001011010000011110101100110010010001110010100010000000010101010010111011010101011011000010010011010110101101011100100101110001100000111110010101100010100010100010000101111000011111000111000011110001110110000011000100110010101111111111100011010000010010010111111110000000010100100101101101010111011000001010000000101011010110011101000110011011001110101101001001101100010011110001101001001000011001101100001101100000101111000001110100001100001000100000000011010011001001011110011000011011000100011011001011100111111000011011010000100000011110110011011110111000001011101101110110101000101011111110000100000111111110011111111100010101001000011010001110111111011100010111001110110001000101010001001001111111110111001101001001000110000110100000000010010100001010111101001110001011101011000100000001001001011111000100011111000011010001110001111111110111100010001110101011101011100010100000011110000100011001100000100111000111011011101000110010011010011110010010000111010001011111111010110011100111011110100111000101100100111001001010001000100011110101100100010000000000110010111101101111101011001101111000000000100000101001011110000010011110011000000100111001001110001000010011111010100001001010010100111111010111001001110110101010010100010010100101100000001010010111101101000110100111110000000111110000011110011001101010111101010111010111010000000110010001011110101110110001000110111101110101101001001100001101110001000100000110100000100000111110010110110010011111100010011111001110111011010101010001011111110000000011110001010011001101010110010101100101100110010111001100100111101000100010100010010100000010010111101100111110101101111101001010110010001111111001101010111110101111001000111101001110100000111111010000111000010101001001101100111001111111111100011010111110001101000100001010000000001101101001110001000001110010000010110001001001101010111111001001010100011011111011000011001001101000110010101000010100001001000011111001101101111011111001000010010111011010110010011010101100100000101100110110011011110000110011000000001011000111100101000011011011010010111000110101110101111100100010101010101000011000111000010001001000100110101111001001001111100110000101100010011101100001000010100010101110001111110101100101000101110000110010100101100101100101100100111111010100101010011100110100011111001000100010001101111111101011110100111001110101001101000010001011000111101110001010100101101111000110101001011101110110110110110101011010001110011111011110011010100110100111111010101111101111100110000110010111110110100110000011110110111111101111010011010000101010111100001111110110000001000001000011101001010010100100100000001101011101110011001011011110010111101111101010011010000110110101000100010110110101101010110110010011010011111111100001001000110111101001111000011001000010111100110001110110011011011100101011010101100011001111111000100000011100110011001001011000100010110000100001100011010000110110011100000111000010001011010001110010101000100010001001110001011001010000111010010101110001010100011101101110010111100010110010000011010111001101000100111011010100001010011100000100001010100010110100111000000001111100000100011100101011011101111111101101110011111010000110111101000001001110111000001000101100110100100111100100011011100010011111101010001101010100101110000110011000100001111100100001000000100011101101011011111000011110010110110101010011101000001111001011100101001001101111000011110000001010011010001110000111001101100011110011001100000111101001011000110111011001101101101100101100110100101011111111110110000111101000000100101011100111001111111011010100110010001000001101010001110010010000101111000001010100000101100000010101110100000000110011001011000011101101000000100111111010111110100011111101100001001110001100101100001010000100000110111101001101010000011100000000100000101101010010101111101100110110111000011100111001010010100101000111011001001110011111100010010010110100111101100110110111001011110010000111011111010101000010001101110011111010110011100010001111111011100110100011110110001101001110001010001110011110101111101011101100000111011011101110000110111101010001000011110011011101100011100101110100000100010110110011010101011000010010110000000100010011001110010011110010110111001111011010101111011000000111110000011011100100010011110010110000001111110111000100111010100110010111100010000110101011110011010110011001011011010010111001000000000001001010101010001100000110111101000000010100100010100101011111110011011100111101001110101010001100000100100110111110001111000011100010110001101101010011001011111101011000110110000111111101100000000001000010010010011101001000111100000010111011011001001100110000101010110001011000001011010111000111100111011010101010011100100100100010000001101001101010111110010100101000001100111110111111110000101111100110001110111010111001111110111100000111011011010111011001111010100010000111011111111000100110110001100000110101000001010010010100111011100000011111110001000010011010101001111010111100011110110110111000000111101010110001100000100001101101001101010111110001101101100101101101001000100000100110111111010011010011111010110110111101001000100010111101100011010111011111010011110000100001100101101111110010101000000101111101000001111110100000001011011111111100100110101101011100101101001011010001100010101101100000101000001110110101010100001011100010000111010011101110000000010000000000010111100111000010000000110110011011101110000001111011100011101111100011000011001000100111010101011010101110011010011011011010100011011000110111101001110011110000100010011000010000001101010010011000111000000000101100011010001000100010100100100011000101110100010001111101001010100001000000110010011101011101000000100010000011010110100111110101110001111001000000101011101010111110110100100011010000011010111111001001111101101110111110111000001010111100010001001001100000000110011100001100100111010011111011001010001101111111000010110101000011100001010110100101110111001001100000000110110101011001110000011001111100001101110100101101111100110001010011011001010110111000100010000110001111101110011100001101000100110000111000110001011011110100010101011011001001111101001110011100001110001010100011001110110101101001101010101001110011110001011101011100100001101100110110110101011101010110011100000001011010111011101000000101110111110010000000000101001110011111011001110001100010111001010010110011100001000011111101111101100111000101011100011000001100000000000010000111111010010101110101011100010100001000000100111111010111110010010111010110010100111000010111100000000100010111010010011010011001100010001000001100110100101110100110110111101010001100001010011111011100000010110110110000000100101100110100101100111001010100010001011010001010011110100110101000110001110000100111111001000110011110010111000110010001111111111101011110100111101001001101110110011111000110010111000011011111001110101101101000011010101011010111101011101111011100101001111111000101100100000011000100101001011001011110001101001100101001"

flist = []
for i in range(101):
    f = []
    for j in output[i:i+100]:
        f.append(int(j))
    flist.append(f)

C = matrix(GF(2), flist[-1])
F = matrix(GF(2), flist[:100])
sol = F.solve_left(C)

flag = ""
for i in sol[0][::-1]:
    flag += str(i)

print(int(flag, 2))

首先提取线性方程系数矩阵 F 和解矩阵 C，而后利用 SageMath 求解方程即可。

其中的 GF(2)，GF 是 Galois Field 的缩写，中文称其为 Galois域或有限域， GF(2)是最简单的有限域，只有0, 1二元及+（异或运算）、×（与运算），大概可以理解为模二运算吧。

在线 SageMath： https://cocalc.com/

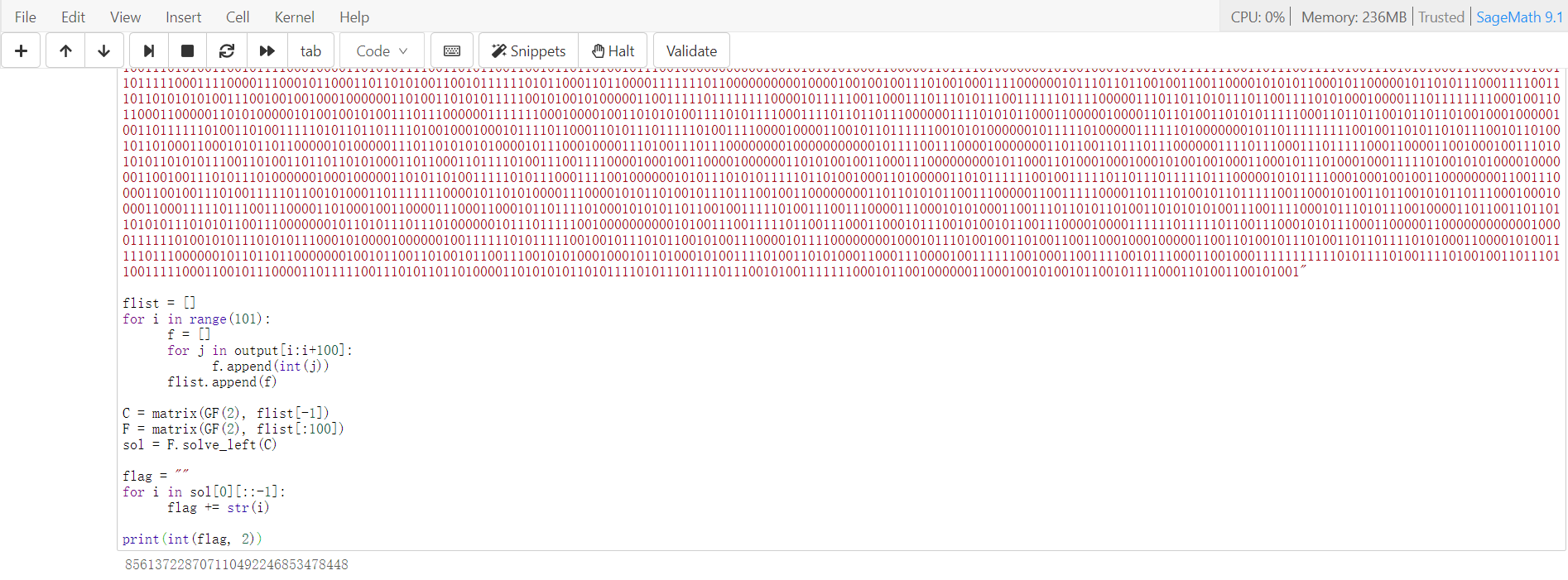
SageMath

flag{856137228707110492246853478448}

SageMath Introduction

这里顺便来介绍一下 SageMath 这一工具喵！

SageMath is a free open-source mathematics software system licensed under the GPL. It builds on top of many existing open-source packages: NumPy, SciPy, matplotlib, Sympy, Maxima, GAP, FLINT, R and many more. Access their combined power through a common, Python-based language or directly via interfaces or wrappers.

Mission: Creating a viable free open source alternative to Magma, Maple, Mathematica and Matlab.

SageMath 是一个基于 GPL 协议的开源数学软件。它使用 Python 作为通用接口，将现有的许多开源软件包整合在一起，构建一个统一的计算平台。

一个数学求解软件，可以解方程啊 balabala，感觉用起来挺爽的。

官网： https://www.sagemath.org/

在线版本： https://cocalc.com/

https://sagecell.sagemath.org/


By the way，这个 CoCalc 能做的不仅仅可以用来跑 SageMath，还有 Jupyter notebook, Linux terminal, X11 desktop, LaTeX document 等等，在线免费用，登录还能保存工作状态，感觉挺实用的呢。

CoCalc

CoCalc2

References & Extensive Reading

（先溜了

文章作者: MiaoTony
文章链接: https://miaotony.xyz/2020/08/27/CTF_2020CISCN_preliminary/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 MiaoTony !
CTF WriteUp Z3
赏
评论
 上一篇
CTF | 2020 GACTF 一点点WriteUp CTF | 2020 GACTF 一点点WriteUp
这几天有个GACTF，随意来看看题目，就佛系做了几个题嘤嘤嘤，顺便来学点东西吧。
2020-08-31 CTF
CTF WriteUp
下一篇 
DSP | CCS v3.3 利用I/O端口从外部文件传送数据的相关配置 DSP | CCS v3.3 利用I/O端口从外部文件传送数据的相关配置
最近做DSP大作业需要用到古老的CCS v3.3软件，而对于利用Simulator的I/O端口从外部文件传送数据的方法，查了各种资料几乎没有相关介绍，正好就来记录一下吧。
2020-07-11 tips
Tech Configuration tips DSP
  目录